分享高职高考数学等差数列求和方法_惠州星华教育高职高考

接下来惠州星华教育老师给大家分享一下高职高考数学等差数列求和方法，希望对大家有用。

等差数列是常见数列的一种，可以用AP表示，如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列，而这个常数叫做等差数列的公差，公差常用字母d表示。
 

等差数列求和公式  

1、公式法

2、错位相减法

3、求和公式

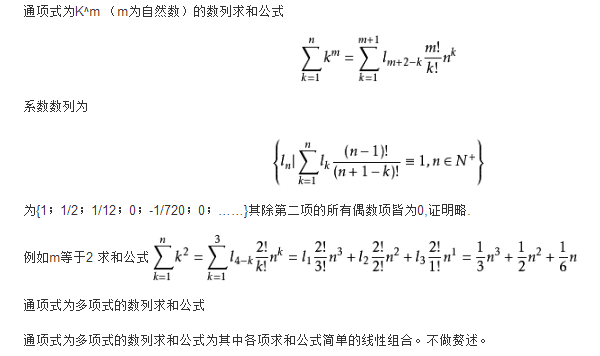
4、分组法
有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.

5、裂项相消法
 适用于分式形式的通项公式，把一项拆成两个或多个的差的形式，即an=f(n+1)－f(n)，然后累加时抵消中间的许多项。

小结：此类变形的特点是将原数列每一项拆为两项之后，其中中间的大部分项都互相抵消了。只剩下有限的几项。
注意：余下的项具有如下的特点
1、余下的项前后的位置前后是对称的。
2、余下的项前后的正负性是相反的。
 
6、数学归纳法
一般地，证明一个与正整数n有关的命题，有如下步骤：
（1）证明当n取第一个值时命题成立；
（2）假设当n=k（k≥n的第一个值，k为自然数）时命题成立，证明当n=k+1时命题也成立。
 
例：
求证：
1×2×3×4 + 2×3×4×5 + 3×4×5×6 + .…… + n(n+1)(n+2)(n+3) = [n(n+1)(n+2)(n+3)(n+4)]/5
 
证明：
当n=1时，有：
1×2×3×4 = 24 = 2×3×4×5/5
 
假设命题在n=k时成立，于是：
1×2x3×4 + 2×3×4×5 + 3×4×5×6 + .…… + k(k+1)(k+2)(k+3) = [k(k+1)(k+2)(k+3)(k+4)]/5
 
则当n=k+1时有：
1×2×3×4 + 2×3×4×5 + 3×4×5×6 + …… + (k+1)(k+2)(k+3)(k+4)
= 1×2×3×4 + 2×3×4*5 + 3×4×5×6 + …… + k(k+1)(k+2)(k+3) + (k+1)(k+2)(k+3)(k+4)
= [k(k+1)(k+2)(k+3)(k+4)]/5 + (k+1)(k+2)(k+3)(k+4)
= (k+1)(k+2)(k+3)(k+4)*(k/5 +1)
= [(k+1)(k+2)(k+3)(k+4)(k+5)]/5
即n=k+1时原等式仍然成立，归纳得证
 
7、并项求和法
（常采用先试探后求和的方法）
例：1－2+3－4+5－6+……+（2n-1）-2n
 
方法一：（并项）
求出奇数项和偶数项的和，再相减。
 
方法二：
（1－2）+（3－4）+（5－6）+……+[（2n-1）-2n]
 
方法三：
构造新的数列，可借用等差数列与等比数列的复合。
an=n(-1)^（n+1）

想了解更多关于高职高考的资讯，可以来星华教育了解一下。