高职高考数学圆锥曲线常见题型总结_惠州星华教育高职高考
admin_hua2022-01-21 14:51:14高职高考常见问题1446来源:高职高考信息网
今天惠州星华教育老师给大家分享一下高职高考数学圆锥曲线常见题型总结,希望能帮到大家。
今天惠州星华教育老师给大家分享一下高职高考数学圆锥曲线常见题型总结,希望能帮到大家。
1、直线与圆锥曲线位置关系
这类问题主要采用分析判别式,有
△>0,直线与圆锥曲线相交;
△=0,直线与圆锥曲线相切;
△<0,直线与圆锥曲线相离.
若且a=0,b≠0,则直线与圆锥曲线相交,且有一个交点.
注意:设直线方程时一定要考虑斜率不存在的情况,可单独提前讨论。
2、圆锥曲线与向量结合问题
这类问题主要利用向量的相等,平行,垂直去寻找坐标间的数量关系,往往要和根与系数的关系结合应用,体现数形结合的思想,达到简化计算的目的。
3、圆锥曲线弦长问题
弦长问题主要记住弦长公式:设直线l与圆锥曲线C相交于A(x1,y1),B(x2,y2)两点,则:
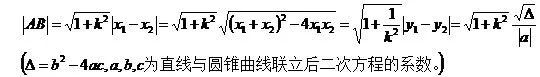
4、定点、定值问题
(1)定点问题可先运用特殊值或者对称探索出该定点,再证明结论,即可简化运算;
(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.
5、最值、参数范围问题
这类常见的解法有两种:几何法和代数法.
(1)若题目的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决,这就是几何法;
(2)若题目的条件和结论能体现一种明确的函数关系,则可首先建立起目标函数,再求这个函数的最值,这就是代数法.
在利用代数法解决最值与范围问题时常从以下五个方面考虑:
(1)利用判别式来构造不等关系,从而确定参数的取值范围;
(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是在两个参数之间建立等量关系;
(3)利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围;
(4)利用基本不等式求出参数的取值范围;
(5)利用函数的值域的求法,确定参数的取值范围.
6、轨迹问题
轨迹问题一般方法有三种:定义法,相关点法和参数法。
定义法:
(1)判断动点的运动轨迹是否满足某种曲线的定义;
(2)设标准方程,求方程中的基本量
(3)求轨迹方程
相关点法:
(1)分析题目:与动点M(x,y)相关的点P(x0,y0)在已知曲线上;
(2)寻求关系式,x0=f(x,y),y0=g(x,y);
(3)将x0,y0代入已知曲线方程;
(4)整理关于x,y的关系式得到M的轨迹方程。
参数法求轨迹的一般步骤:
(1)选取参数k,用k表示动点M的坐标;
(2)得动点M的轨迹的参数方程

(3)消去参数k得的M轨迹方程;
(4)由k的范围确定x,y的范围,确保答案的准确性和完备性。
7、探索型,存在性问题
这类问题通常先假设存在,然后进行计算,最后再证明结果满足条件得到结论。对于较难的题目,可从特殊情况入手,找到特殊点进行分析验算,然后再得到一般性结论。
圆锥曲线简化技巧
1、给定一个椭圆和一条直线:
椭圆方程:
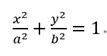
直线方程:y=kx+b
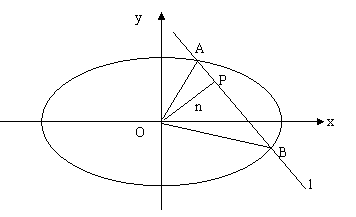
一般做法:

上面的运算数不是有点复杂呢,那接着往下看看小编提供的计算技巧吧:
巧运算:
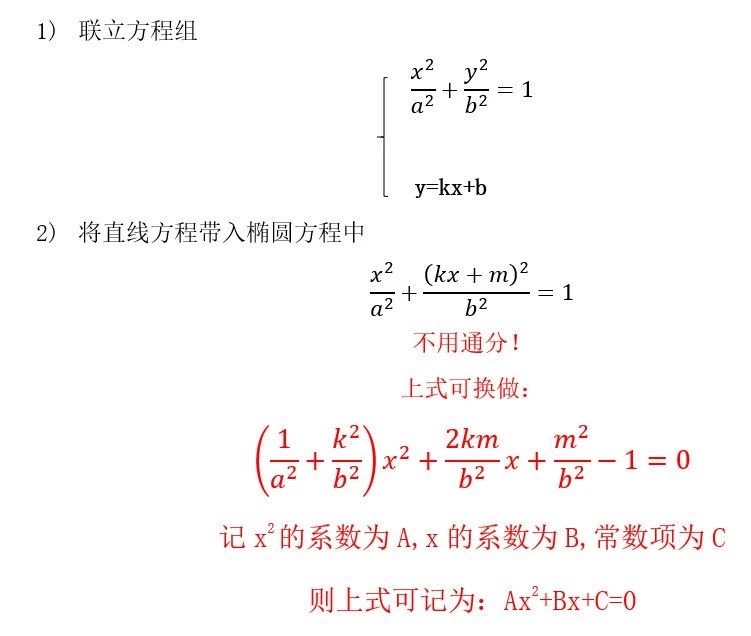

2、此外,常用的两个结论还有:
1、直线交椭圆的弦长:
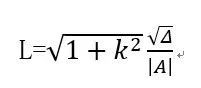
(因为只要联立了方程组,就一定要求判别式,将判别式代入这个式子求弦长会比一般做法简单很多)
2、y1+y2=k(x1+x2)+2m
y1y2=k2x1x2+km(x1+x2)+m2
用此方法可大幅节省运算时间,圆锥曲线是不是简单了不少呢?
圆锥曲线公式集锦
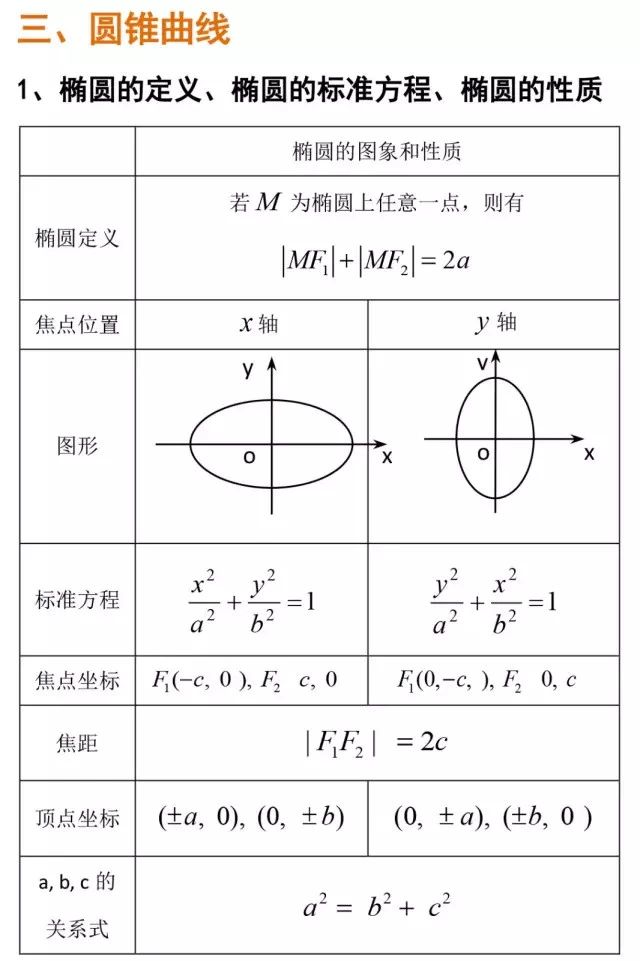
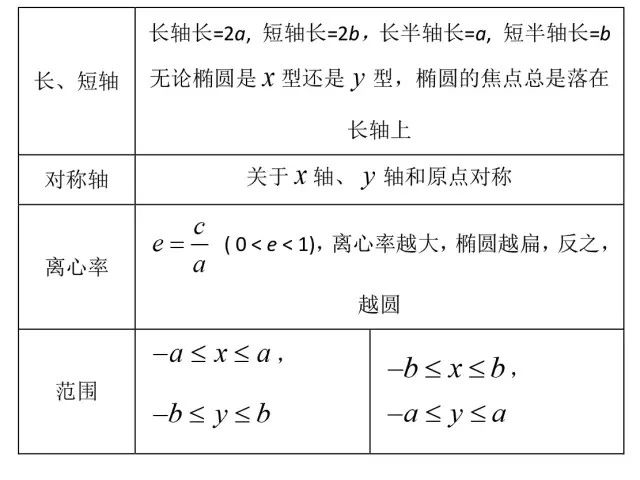




 想了解更多关于高职高考的资讯,可以来星华教育了解一下。
想了解更多关于高职高考的资讯,可以来星华教育了解一下。
相关文章
- 韩山师范学院-2023年春季高考招生简章-学校简介
- 汕尾职业技术学院可以转专业吗-大专入学时可以转专业吗-专业分析-医疗医药类专业好不好-北大青鸟计算机编程培训
- 广东松山职业技术学院能不能转专业-大专转专业一般在什么时候-专业分析-管理类专业好不好-北大青鸟计算机职业学校
- 罗定职业技术学院好转专业吗-大专被不喜欢的专业录取了,怎么办-专业分析-化学类专业好不好-北大青鸟计算机考试培训
- 广东茂名健康职业学院转专业难吗-大专转专业是什么时间-专业分析-计算机类专业好不好-北大青鸟计算机设计培训
- 广东梅州职业技术学院入学时可转专业吗-大专可以转专业吗-专业分析-医疗医药类专业好不好-北大青鸟计算机网络培训
- 惠州城市职业学院可以转专业吗-大专入学时可以转专业吗-专业分析-新能源类专业好不好-北大青鸟计算机编程培训
- 广东环境保护工程职业学院能不能转专业-大专转专业一般在什么时候-专业分析-化学类专业好不好-北大青鸟计算机职业学校





 微信收款码
微信收款码 支付宝收款码
支付宝收款码